大学三大数学关系

高中数学参考

http://www.sohu.com/a/142139848_228459?loc=2&cate_id=16

大学数学三大分支

微积分:

我们在初中高中的时候, 学到的是一些简单的图形的面积, 周长.比如三角,圆.
但如果要求更复杂的图形. 比如正态分布, 椭圆, 贝塞尔曲线,我们就需要借助微积分.
这只是一个数学的进化过程,从简单的线性到复杂的线性.

线性代数

目的是用来求解行列式(方程组). 或者空间向量转换.

概率统计

这应该是最有用的一门课. 不论是金融、人工智能、都逃不开它。
个人理解：其实微积分几乎完全为它服务。

连接三大分支的核心–最小二乘法

假设一组数据
X Y
21.6 208
15.5 152
10.4 113
31.0 227
13.0 137
32.4 238
19.0 178
10.4 104
19.0 191
11.8 130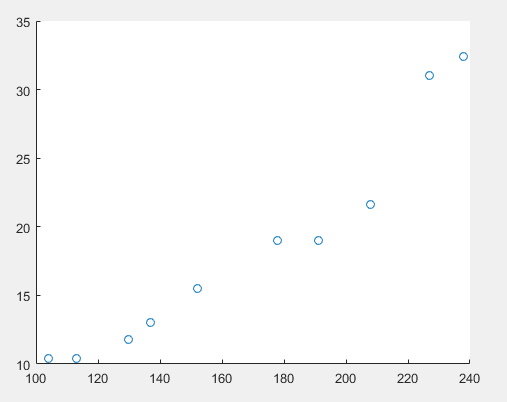

假设公式为 y=kx+b; 也就是我们假设这是一条直线.
要求一条直线,离这些点最近. 引入方差概念.

对上式求偏导(微积分)

x2=sum(X.^2); % 求Σ(xi^2)
x1=sum(X); % 求Σ(xi)
x1y1=sum(X.Y); % 求Σ(xiyi)
y1=sum(Y); % 求Σ(yi)
k=(nx1y1-x1y1)/(nx2-x1x1); %解出直线斜率b=(y1-ax1)/n
b=(y1-ax1)/n; %解出直线截距

求解出k=0.1612 b=-8.6451 (事实上,这步求解都是用矩阵完成)
y=x*0.1612-8.6451;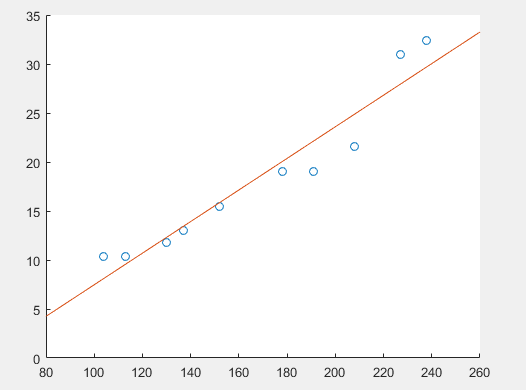

more

当我们把公式变成Y=aX^2 + bx +c的时候